Nárůst Stability při opakování

Metoda RE-WISE tedy doporučuje uživateli, aby si Fakt zopakoval, když ho částečně zapomene, asi tak o 30%.

Předpokládáme, že po opakování si budeme pamatovat Fakt už déle, v průměru dvakrát déle. V předchozím návrhu vzorce jsme se snažili, aby Stabilitu bylo možné interpretovat jako počet dní do příštího doporučeného opakování.

• STAB_n je Stabilita v n-tém opakování.

Znovu zdůrazněme, že vzoreček platí pouze tehdy, když žák opakuje v optimálním okamžiku.

Jak bude v takovém optimálním případě vypadat průběh Retrievability? Po každém opakování vyskočí vždy na 100% a potom bude postupně klesat. Klesání bude po každém opakování pomalejší.

Příklad:

Použijme navrhované vzorečky pro RET a STAB.

Zvolme OFI = 30%. Tedy budeme opakovat vždy, když RET poklesne pod 70%.

Potom bude křivka zapomínání vypadat takto:

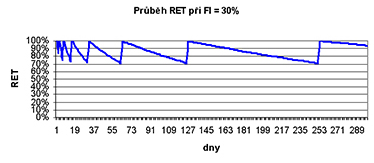
Poznámka: Klesající části křivky nejsou přímky, ale úvodní části hodně narovnané převrácené exponenciály – křivky 1/2(^m*SN/STAB.

Základ geometrické řady (Base Factor)

Proč by se měla Stabilita v okamžiku optimálního opakování zvýšit zrovna 2x? Proč ne třeba 2,2x nebo 1,5x? Každé slovíčko je jinak těžké a také každý člověk má jinou paměť. Nahradíme tedy dvojku ve vzorečku pro výpočet Stability parametrem a nazveme ho Base Factor. Na začátku výuky budeme předpokládat, že má hodnotu 2 a budeme se jeho hodnotu snažit určit z průběhu opakování. O tom ale až za chvíli.

• n je počet opakování
• Base Factor je nějaké číslo, které vychází z obtížnosti Faktu a paměti žáka a obvykle bývá tak kolem hodnoty 2.

Iniciální Stabilita (iniStab)

Můžeme se opět ptát, proč by počáteční hodnota Stability měla být zrovna 1.

Představme si, že se už nějaký čas metodou RE-WISE učíme, dosáhneme u Faktu Stability 20. Base Factor (základ geometrické řady, kterou se zvyšuje Stabilita), je ale stále 2, protože Fakt je pořád stejně – průměrně – těžký.

Najednou ouha – zkolabuje disk a my přijdeme o data. Začneme se ovšem statečně učit znovu. Opakujeme po jednom, dvou, čtyřech dnech a odpovídáme stále správně, nezapomínáme. Pokud by algoritmus upravoval jen hodnotu Base Factor, usoudil by, že je Fakt pro nás moc lehký a začal by Base Factor zvyšovat. To ale není dobře. Fakt je stále stejně těžký, jen jsme ho na začátku už trochu uměli. Algoritmus by měl po čase uhodnout, že správná hodnota Base Factor je stále 2, ale že měl vlastně začít od hodnoty Stability 20.

Zavedeme tedy ještě jeden parametr pro obtížnost Faktu. Nazveme ho Iniciální Stabilita (iniStab) a budeme na začátku předpokládat, že má hodnotu 1.

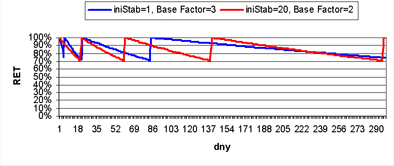
Graf srovnává průběh křivky opakování pro zvýšený parametr Base Factor proti zvýšení iniStab. Křivka s vyšším Base Factor vždy po čase předběhne křivku s vyšší hodnotou iniStab. To má doložit tvrzení, že úpravou jednoho parametru nedokážeme kompenzovat změnu druhého a že bychom se proto měli snažit hledat vhodnou kombinaci obou.

Změna stability (CHNG)

Navržený vzoreček, jak jsme několikrát zdůraznili, platí pouze tehdy, když se opakuje v optimálním okamžiku. Předpokládáme, že tento okamžik nastane tehdy, když Fakt zapomeneme o 30%.

Co se ale stane, když budeme Fakt opakovat jindy než v tomto optimálním okamžiku? Stabilita se zvýší pokaždé jinak v závislosti na okamžité hodnotě Retrievability.

• CHNG(RET_n, Base Factor) je funkce závislá na velikosti Retrievability v okamžiku opakování. Maximálně dosahuje hodnoty Base Factor.
• RET_n je skutečná hodnota Retrievability, kterou odhadneme z bodového hodnocení v daném opakování. Body může přidělit program, pokud umí odpověď automaticky vyhodnotit, nebo můžeme požádat žáka, aby sám ohodnotil, nakolik si Fakt pamatoval.
• IniStab a Base Factor jsou čísla, která charakterizují obtížnost Faktu. Na začátku předpokládáme, že mají hodnoty IniStab=1 a Base Factor=2. Budeme se je ale snažit adaptovat podle průběhu opakování. Detaily adaptace přijdou později, nejdříve ještě musíme přesněji definovat funkci CHNG.

Tvar funkce CHNG

Jak by měla funkce vypadat funkce, která řekne na základě Retrievability, kolikrát se zvýší Stabilita?

Pro návrh jejího tvaru máme tři hypotézy:

• První hypotéza o změně Stability říká: „Pokud opakuji Fakt rychle za sebou (při vysoké Retrievability), Stabilita se moc nezvyšuje“. To je možné vyjádřit tak, že pokud se Retrievability blíží 100%, bude se změna CHNG blížit 1:

lim_RET->100%CHNG(RET) = 1

• Druhá hypotéza o změně Stability říká: „Pokud Fakt opakuji s vhodným časovým odstupem, Stabilita stoupá“. To lze při troše fantazie interpretovat tak, že existuje optimální míra zapomenutí (OFI), při které CHNG nabývá maxima. Toto maximum by mělo být rovno Base Factor (tak asi 2):

Base Factor = CHNG(100%-OFI) >= CHNG(RET)_{0 <= RET <= 100%}

• Třetí hypotéza říká: „Po zapomenutí Faktu (pokles Retrievability pod jistou mez), Stabilita rychle mizí.“ Tedy pokud se Retrievability blíží k 0%, změna Stability se také blíží k 0.

lim_RET->0CHNG(RET) = 0

Mezi těmito body navrhujeme natáhnout vhodnou křivku, která by byla souvislá a pěkně zaoblená. Tyto požadavky by mohla například splnit funkce složená ze dvou parabol. Obě mají vrchol v bodě 1-OFI, jedna z nich prochází bodem (0,0), druhá bodem (1,1).

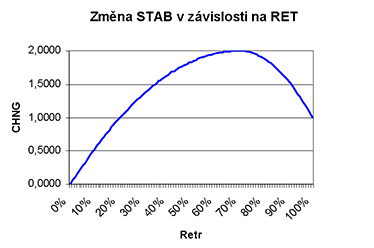
Kritický čtenář může v tomto okamžiku namítnout, že jsme si vymysleli křivku na základě hodnot funkce ve třech bodech. Na to lze říct například to, že hodnoty Retrievability s přesností na procento se od uživatele stejně nedozvíme. V metodě RE-WISE se uživatel hodnotí obvykle na škále 0-4 body, tedy velmi hrubě. Proto snad na přesném tvaru křivky tolik nezáleží.

Odvodit vzoreček pro tyto paraboly je nudná středoškolská dřina, kterou se neodvažujeme čtenáře zatěžovat.

Omezíme se tedy na konstatování, že vzoreček pro parabolu je:

y = Ax² + Bx + C

Dále známe hodnotu každé paraboly ve dvou bodech – na kraji a ve vrcholu.

• Pro RET = 0 má vyjít 0.
• Pro RET = 1 má vyjít 1.
• Pro RET = 1 - OFI má vyjít maximum – Base Factor.

Kromě toho víme, že v bodě 1- OFI mají obě funkce maximum, tedy jejich první derivace je nulová.

To už je spousta rovnic na to, abychom jistým úsilím dospěli k hodnotám koeficientů:

A₁ = (1 - Base Factor) / OFI²

B₁ = -2 * (1 - OFI) * A₁

C₁ = 1 - (1 - 2 * (1 - OFI)) * A₁

A₂ = -Base Factor / (1 - OFI)²

B₂ = -2 * (1 - OFI) * A²

C₂ = 0

Navrhli jsme tedy vzorec, který modeluje zapomínání naučených Faktů. Vzoreček nám dokonce umožňuje předpovědět, jaké hodnocení dostane žák při příštím opakování. Co ale uděláme, když žák dostane bodů více nebo méně? Chtěli bychom náš vzoreček nějak přizpůsobit skutečným výsledkům a další předpovědi tím zpřesnit. Tím se zabývá odstavec Adaptace podle známkování.